חלק שביעי: אקורדים עם שינויים - אקורדים מוקטנים Diminished Chords

הסימון של אקורדים מוקטנים:

התבנית של אקורדים מוקטנים:

התבנית של אקורד מוקטן היא:   -Xdim7=1  3-  5-  7 

לפני שנראה כיצד לבנות את האקורד על צוואר הגיטרה ומהן התכונות המייחדות סוג זה של אקורדים, הבה נבנה שתי טבלאות: באחת נציג את התווים של הספטאקורדים המז'וריים ובשנייה את תוויהם של האקורדים המוקטנים:

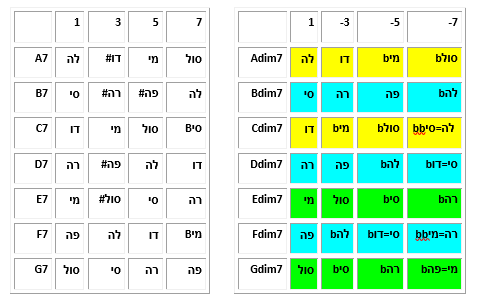
עת, אם נתבונן באקורדים שהרקעים שלהם זהים בצבעם נגלה להפתעתנו שקיבלנו בדיוק את אותם אקורדים, שכן התווים שלהם זהים לחלוטין. מכאן אנו מקבלים את הזהויות הבאות::

Adim7=Cdim7

Bdim7=Ddim7=Fdim7

Edim7=Gdim7

 למעשה מספרן של הזהויות בין האקורדים המוקטנים עוד יותר גדול מכך כפי שנראה מהכלל הבא.

הכלל הראשון של האקורדים המוקטנים:

אם ניקח כל אחד מתוויו של אקורד מוקטן ונבנה עליו אקורד מוקטן חדש שהתו הנבחר הוא השורש שלו, נקבל את אותו אקורד מוקטן.

 הבה נבדוק זאת על האקורד Adim7, שתוויו הם לה, דו, מיb, סולb.

נבנה אקורד מוקטן על דו ונקבל: 

 לה  סולb  מיb  דו = Cdim7

כלומר את אותו האקורד.

נבנה אקורד מוקטן על מיb ונקבל: 

 דו  לה  סולb  מיEbdim7 = b

כלומר את אותו האקורד.

נבנה אקורד מוקטן על סולb ונקבל:

מיb דו לה סולGbdim7 = b

כלומר את אותו האקורד.

כמו שרצינו להוכיח, קיבלנו בכל המקרים את אותו אקורד עצמו.

כעת אנו יכולים על סמך זאת להרחיב את מערכת המשוואות הקודמות ולקבוע כי:

Adim7=Cdim7=Ebdim7=D#dim7*=Gbdim7=F#dim7

Bdim7=Ddim7=Fdim7=Abdim7=G#dim7

Edim7=Gdim7=Bbdim7=A#dim7=Dbdim7=C#dim7

*Ebdim7=D#dim7  כי מי במול שווה לרה דיאז

מכאן שלמעשה קיימים רק שלושה אקורדים מוקטנים, וכל אקורד מוקטן הוא אחד משלושה אקורדים אלה.

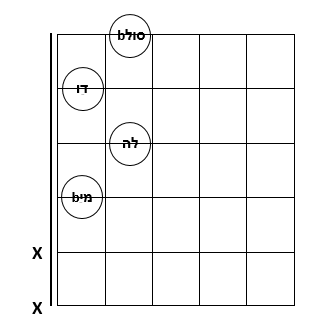
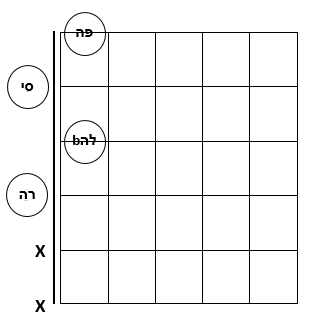
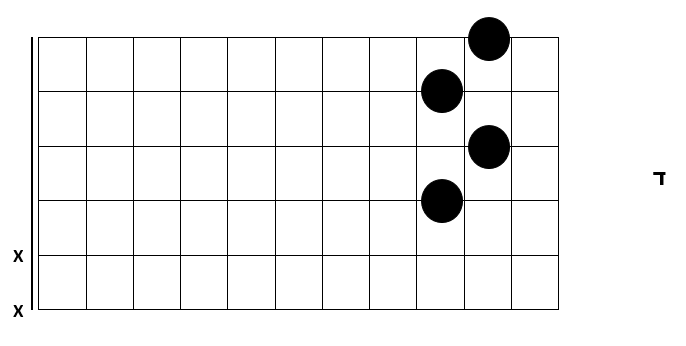
עכשיו נבנה מכל אחד מהאקורדים הללו אקורד מוקטן על צוואר הגיטרה. נבנה אותם באותה שיטה שבה בנינו את האקורדים הבסיסיים, כלומר נעבור מיתר אחרי מיתר ממיתר ראשון והלאה ונסמן את הפוזיציה הראשונה שבה יופיע אחד מתווי האקורד, אך שלא כמו שם, נעצור כשנקבל את כל ארבעת תווי האקורד. נבנה אקורד מוקטן מהקבוצה של Adim7:  נבנה אקורד מוקטן מהקבוצה של Bdim7: 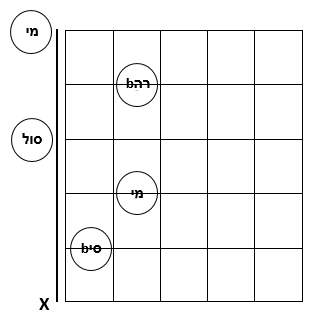נבנה אקורד מוקטן מהקבוצה של Edim7:

זה הזמן להכיר את הכלל הבא (כלל זה נובע מהכלל הראשון).

הכלל השני של האקורדים המוקטנים:

כדי לדעת היכן להניח את האצבעות כדי לקבל אקורד מוקטן ספציפי, עלינו להניחן כך שאחת האצבעות (ולא חשוב איזו) מונחת בפוזיציה שבה מופיע שורש האקורד.

מהתוצאות שקיבלנו אנו רואים שאם ניקח אקורד מוקטן מהקבוצה של Bdim7 (סי, רה, פה, להb) ונעלה את תוויו בחצי טון נקבל אקורד מוקטן מהקבוצה של Adim7 (לה, דו, מיb, סולb). אם נעלה שוב בחצי טון נקבל אקורד מוקטן מהקבוצה של Edim7 (מי, סול, סיb, רהb), וחצי טון נוסף יעלה אותנו חזרה לקבוצה של Bdim7.

הכלל השלישי של האקורדים המוקטנים:

כל אקורד מוקטן יחזור על עצמו שלוש פוזיציות מעל הפוזיציה שבה הוא נמצא.

כלל זה מציג את אחת התכונות המופלאות של האקורדים המוקטנים. תכונה זו מאפשרת לנו לגוון את הנגינה, במקום בו מופיע אקורד מוקטן, ניתן לנגן את אותו אקורד במספר פוזיציות שונות וכך לגוון את הנגינה. כך למשל במקום לנגן את Fdim7 במקום יחיד למשך כל זמן הנגינה שלו, למשל כך:

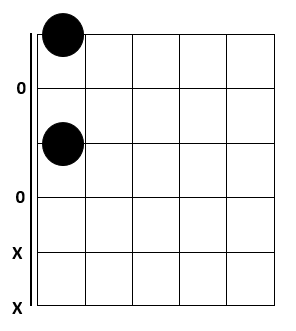ניתן לחלק את זמן הנגינה ולנגן את אותו אקורד במספר פוזיציות שונות: 

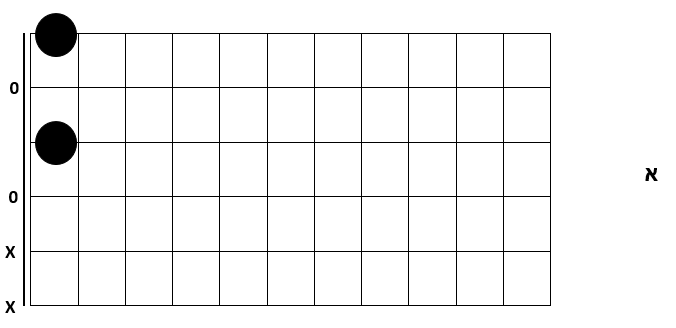
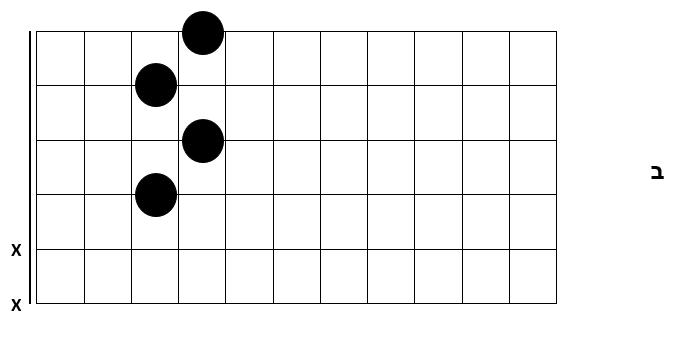
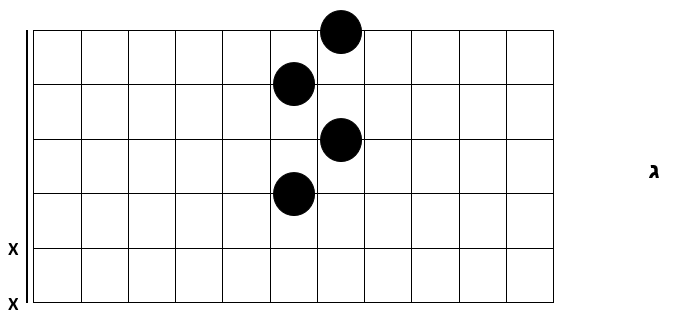
ביצוע המעבר בצורה זו נשמע מעניין הרבה יותר מנגינת האקורד בפוזיציה אחת.